世上最伟大的十个公式 质能方程让人类颤抖60年(2)

圆周长公式

　　创立者：祖冲之(所以国际上也称“祖率”)

　　提出时间：南北朝

　　意义：精确计算圆周长、圆面积、球体积等几何形状的关键值。也可应用于工程师或物理学家要进行较精密的计算

　　公式：

　欧拉公式(Euler’s Identity)

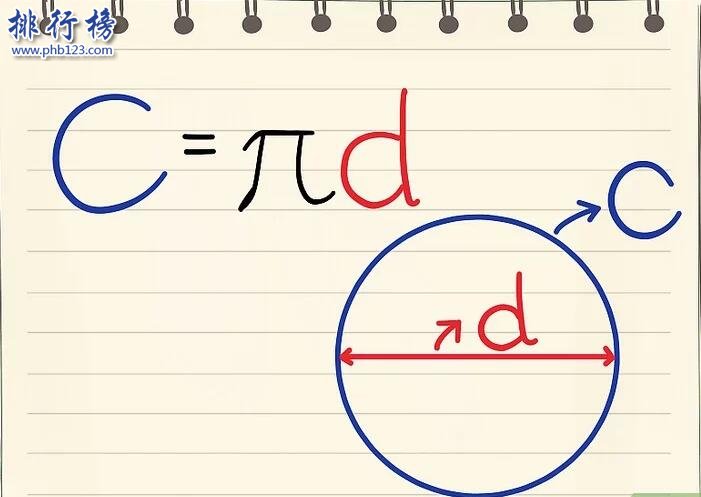
　　创立者：莱昂哈德·欧拉

　　提出时间：1752年

　　欧拉公式也被称为世界上最完美的公式，在数学历史上有很多公式都是欧拉发现的，它们都叫做欧拉公式，它们分散在各个数学分支之中。如：分式里的、复变函数论里的、三角形中的、拓扑学里的、初等数论里的欧拉公式等等。以下举例：

　　(1)分式里的欧拉公式：

　　a^r/(a-b)(a-c)+b^r/(b-c)(b-a)+c^r/(c-a)(c-b)

　　当r=0,1时式子的值为0 当r=2时值为1

　　当r=3时值为a+b+c

　　(2)复变函数论里的欧拉公式：

　　e^ix=cosx+isinx，e是自然对数的底，i是虚数单位。它将三角函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位.

　　将公式里的x换成-x，得到：

　　e^-ix=cosx-isinx，然后采用两式相加减的方法得到：

　　sinx=(e^ix-e^-ix)/(2i)，cosx=(e^ix+e^-ix)/2.这两个也叫做欧拉公式。将e^ix=cosx+isinx中的x取作∏就得到：

　　e^i∏+1=0. 这个恒等式也叫做欧拉公式，它是数学里最令人着迷的一个公式，它将数学里最重要的几个数学联系到了一起：两个超数：自然对数的底e，圆周率∏，两个单位：虚数单位i和自然数的单位1，以及数学里常见的0。数学家们评价它是“上帝创造的公式”，我们只能看它而不能理解它。

　　(3)三角形中的欧拉公式：

　　设r为三角形外接圆半径，r为内切圆半径，d为外心到内心的距离，则： d^2=r^2-2rr

　　(4)拓扑学里的欧拉公式：

　　v+f-e=x(p)，v是多面体p的顶点个数，f是多面体p的面数，e是多面体p的棱的条数,x(p)是多面体p的欧拉示性数。

　　如果p可以同胚于一个球面(可以通俗地理解为能吹胀而绷在一个球面上)，那么x(p)=2，如果p同胚于一个接有h个环柄的球面，那么x(p)=2-2h。

　　x(p)叫做p的欧拉示性数，是拓扑不变量，就是无论再怎么经过拓扑变形也不会改变的量，是拓扑学研究的范围。

　　在多面体中的运用:

　　简单多面体的顶点数v、面数f及棱数e间有关系

　　v+f-e=2

　　这个公式叫欧拉公式。公式描述了简单多面体顶点数、面数、棱数特有的规律。

　　(5)初等数论里的欧拉公式：

　　欧拉φ函数：φ(n)是所有小于n的正整数里，和n互素的整数的个数。n是一个正整数。

　　欧拉证明了下面这个式子：

　　如果n的标准素因子分解式是p1^a1*p2^a2*……*pm^am，其中众pj(j=1,2,……,m)都是素数，而且两两不等。则有

　　φ(n)=n(1-1/p1)(1-1/p2)……(1-1/pm)

　　利用容斥原理可以证明它。

　　此外，还有很多著名公式都以欧拉命名哦，它不仅是世界上最伟大十大公式之一，也是数学里最令人着迷的公式之一，也是最美的，因为这个公式的精简。它没有多余的字符，却联系着几乎所有的数学知识。

免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。